by Alain Busser
Compact non-orientable surfaces: Parametric Representations
To view these images, you need RED-CYAN anaglyph glasses. For the best experience, turn the files with the cursor keys.
No, this is not the name of my rock band, but A. Möbius gave his name to the first model of a non-orientable surface in the middle of XIXth century:
>u=linspace(-1,1,10); ... v=linspace(0,2*pi,50)'; ... X=(3+u*cos(v/2))*cos(v); Y=(3+u*cos(v/2))*sin(v); Z=u*sin(v/2);
The following is an anaglyph. You will need red/cyan glasses to view this image properly.
>wirecolor(gray); plot3d(X,Y,Z,>anaglyph,<frame,scale=1.7):

But any odd number of half-turns would lead to a non-orientable surface, homeographic to the model above. For example, replace "v/2" by "3*v/2" and you'll see 3 half-turns:
>u=linspace(-1,1,100); ... v=linspace(0,2*pi,100)'; ... X=(3+u*cos(3*v/2))*cos(v); Y=(3+u*cos(3*v/2))*sin(v); Z=u*sin(3*v/2); ... plot3d(X,Y,Z,>anaglyph,<frame,scale=1.8,grid=[10,5]):

The border of this Möbius band is none the less than a trefoil knot:
>plot3d("(3+cos(3*x/2))*cos(x)","(3+cos(3*x/2))*sin(x)","sin(3*x/2)", ...
xmin=0,xmax=4*pi,>anaglyph,<frame,scale=1.8):
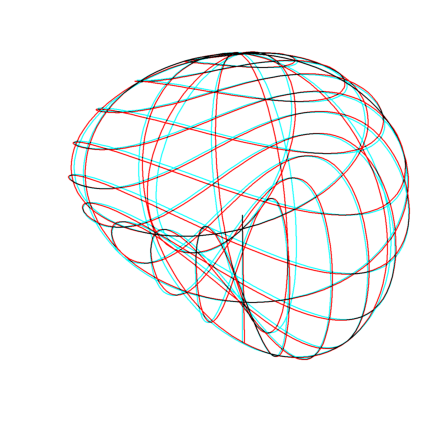
If one tries to close a non-orientable surface (reducing its border to a point), a self-intersection is unavoidable. So the compact non-orientable surfaces without border are always self-intersecting in R^3. Their characteristic is an integer inferior to 2. In some sense, the simplest one could be the one with characteristic one:
If one sews the border of a one-half-turn Möbius band against the circle of a semi-sphere, one gets a surface looking like a bishop's hat, which french name is a "mitre". (Be careful though that in PovRay's example the name of "mitre" is given to an orientable surface). This model of the projective plane has been found by J. Steiner near the end of the XIXth century:
>u=linspace(0,2*pi,100); ... v=linspace(0,pi/2,50)'; ... X=1/2*cos(u)*sin(2*v); Y=1/2*sin(u)*sin(2*v); ... Z=1/2*(cos(v)^2-(sin(v)*cos(u))^2); ... plot3d(X,Y,Z,n=20,<frame,>anaglyph,scale=1.5,angle=40°, ... >transparent,grid=10):
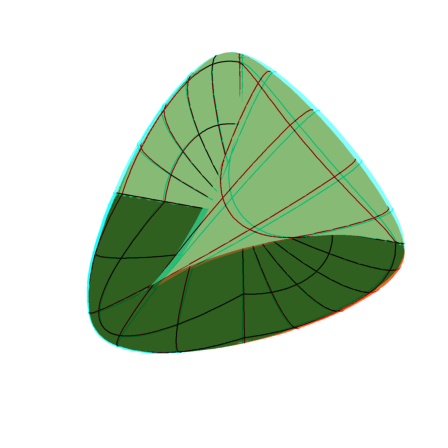
Here is a cut version of this object.
>u=linspace(0,pi,100); ... v=linspace(0,pi/2,50)'; ... X=1/2*cos(u)*sin(2*v); Y=1/2*sin(u)*sin(2*v); ... Z=1/2*(cos(v)^2-(sin(v)*cos(u))^2); ... plot3d(X,Y,Z,n=20,<frame,>anaglyph,scale=1.7,angle=40°, ... >hue,grid=10):

This surface, whose english name is "crosscap" (source: Eric Weisstein), is a quartic. If now one sews a 3-half-turns Möbius band against the border of a disk, one gets the most symmetrical of all non-orientable surfaces: THE FAMOUS STEINER ROMAN SURFACE (with the rolling drums...):
>u=linspace(0,pi,100); ... v=linspace(0,pi,50)'; ... X=1/2*sin(2*u)*sin(v)^2; Y=1/2*sin(u)*sin(2*v); Z=1/2*cos(u)*sin(2*v); ... plot3d(X,Y,Z,>anaglyph,n=100,frame=0,scale=1.5,grid=10):
This is a quartic too.
Steiner had an impressive collection of parametric models of the
projective plane, but he seems to have missed this one, that I found
empirically:
>u=linspace(0,2*pi,100); ... v=linspace(-pi/2,pi/2,50)'; ... X=cos(u)*cos(v); Y=sin(u)*cos(v); Z=sin(2*v)*cos(3*u/2); ... plot3d(X,Y,Z,anaglyph=1,n=20,<frame,height=60°, ... scale=1.5,grid=10):

This surface should maybe be called "the Busser decic" because its implicit equation has degree 10.
All the Steiner models have self-intersection sets composed of segments. At the very beginning of the XXth century, D. Hilbert asked his students to try and prove that any model of the projective plane shares this property. One of them, called Boy, came up with this now famous counterexample, also found by sewing a 3 half-turn Möbius band against a hemisphere:
>u=linspace(0,2*pi,100); ... v=linspace(0,pi,50)'; ... m=3; c0=2; c1=0.5; c2=0.5; r=4; ... a=c0+c1*sin(2*m*v-pi/3)+c2*sin(m*v-pi/6); ... b=c0+c1*sin(2*m*v-pi/3)-c2*sin(m*v-pi/6); ... alpha=pi/8*sin(m*v); ... x1=(a^2-b^2)/sqrt(a^2+b^2)+a*cos(u)-b*sin(u); ... z1=sqrt(a^2+b^2)+a*cos(u)+b*sin(u); ... X=r*(x1*cos(v)-z1*sin(alpha)*sin(v)); ... Y=r*(x1*sin(v)+z1*sin(alpha)*cos(v)); ... Z=r*z1*cos(alpha); ... plot3d(X,Y,Z,>anaglyph,<frame,scale=1.5,grid=20):

This model originates to J.P. Petit and J. Souriau, and was modified by J.F. Colonna. On wikipedia there is a slightly different parametric equation. Apery found a cartesian equation for this surface, making it an octic.
But no one seems to have tried before to sew a 5-half-turns Möbius band against a hemisphere, which leads to a Boy-like surface with 5 branches, and is quite new (it has no name):
>u=linspace(0,2*pi,100); ... v=linspace(0,pi,60)'; ... m=5; c0=2; c1=0.5; c2=0.5; r=4; ... a=c0+c1*sin(2*m*v-pi/3)+c2*sin(m*v-pi/6); ... b=c0+c1*sin(2*m*v-pi/3)-c2*sin(m*v-pi/6); ... alpha=pi/8*sin(m*v); ... x1=(a^2-b^2)/sqrt(a^2+b^2)+a*cos(u)-b*sin(u); ... z1=sqrt(a^2+b^2)+a*cos(u)+b*sin(u); ... X=r*(x1*cos(v)-z1*sin(alpha)*sin(v)); ... Y=r*(x1*sin(v)+z1*sin(alpha)*cos(v)); ... Z=r*z1*cos(alpha); ... plot3d(X,Y,Z,>anaglyph,<frame,scale=1.5,height=60°,grid=20):

This can be generalized to 7, 9, 11 etc. halfturns (until an overflow...)
Now to the next compact non-orientable surface without a border, discovered by F. Klein at the very end of the XIXth century:
The Klein bottle is obtained in sewing two Möbius bands, border to border. If the 2 borders have 1 half-turn, it leads to either the Banchoff model (see below) or the famous Etruscan venus:
>u=linspace(0.001,2*pi,100); ... v=linspace(0.001,2*pi,50)'; ... a=4; b=2; c=2; e=3; g=12; ... w=b*sin(u)+e; ... dx=a*cos(u)-a*cos(c*u); ... dy=-g*sin(u); ... rxy=sqrt(dx^2+dy^2); ... X=a*sin(u)-b*sin(c*u)-dy*w*cos(v)/rxy; ... Y=g*cos(u)+dx*w*cos(v)/rxy; ... Z=w*sin(v); ... plot3d(X,Y,Z,>anaglyph,<frame,scale=2,angle=180°,grid=20):
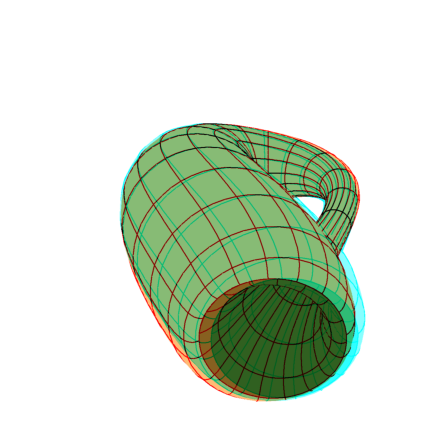
This parametric representation is due to P. Jeener (a different one can be found on wikipedia). P. Jeener generalized his parametric representation to the case where the bottle has any odd number of necks (see Colonna's web site at the Ecole Polytechnique). What he found has been ameliorated by E. Bonan; which leads to this beautiful 3-necks Klein bottle:
>u=linspace(0,2*pi,100); ... v=linspace(0,2*pi,50)'; ... s=2; t=4; ... w=(s+1)/4*cos((s+1)*u+pi/t)+sqrt(2); ... X=s*cos(u)+cos(s*u)-w*sin((s-1)/2*u)*cos(v); ... Y=s*sin(u)-sin(s*u)-w*cos((s-1)/2*u)*cos(v); ... Z=w*sin(v); ... plot3d(X,Y,Z,anaglyph=1,n=20,frame=0,scale=1.8):

Prosit, prosit , prosit!
If one sews two Möbius bands on the extremities of a cylinder, one gets more simple surfaces with 2 crosscaps. The following example is a special case of Jeener-Bonan model:
>u=linspace(0,2*pi,50); ... v=linspace(0,2*pi,100)'; ... s=0; t=2; ... w=(s+1)/4*cos((s+1)*u+pi/t)+sqrt(2); ... X=s*cos(u)+cos(s*u)-w*sin((s-1)/2*u)*cos(v); ... Y=s*sin(u)-sin(s*u)-w*cos((s-1)/2*u)*cos(v); ... Z=w*sin(v); ... plot3d(X,Y,Z,>anaglyph,<frame,scale=1.5,grid=20,>transparent):
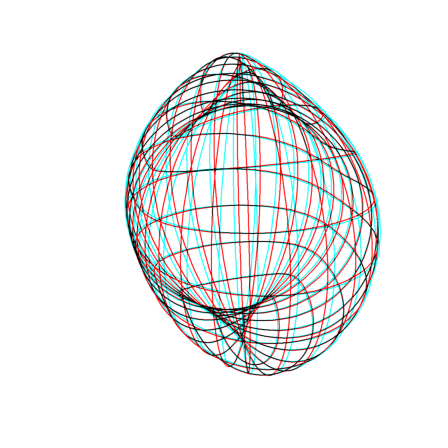
Its shape reminds an x-rated fruit from the Seychelles islands...
The following model has been found by Alain Busser (that's me!)
>u=linspace(0,2*pi,100); ... v=linspace(-pi/2,pi/2,50)'; ... X=1/2*cos(u)*cos(v); Y=1/2*sin(u)*cos(v); Z=1/2*sin(v)-cos(u)^2*sin(v/2)^3; ... plot3d(X,Y,Z,>anaglyph,<frame,scale=1.5,>hue,grid=40):

This surface has an implicit equation but its degree is 24 (d'uh!)
Would you be enable to find a model of whatever one obtains sewing 3 or 5 half-turn Möbius bands against the borders of a cylinder?
Anyway J.P. Petit (whose name happens to translate as "Klein" in german...) found a way to group the pinchs at the center of his surface:
>u=linspace(0,2*pi,100); ... v=linspace(0,pi,50)'; ... X=(1+sin(v))*cos(u); Y=2*sin(u)*sin(v); Z=sin(2*v); ... plot3d(X,Y,Z,anaglyph=1,n=20,frame=0,scale=1.5,>transparent,grid=20):
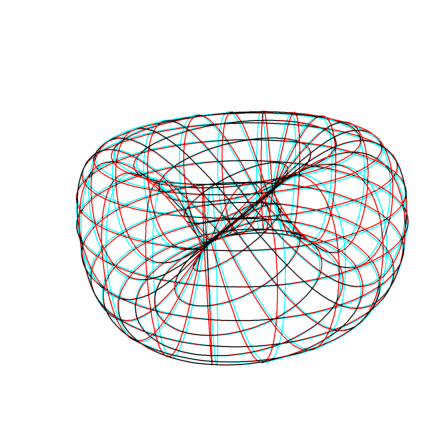
Here is cut version of this.
>u=linspace(pi,2*pi,100); ... v=linspace(0,pi,50)'; ... X=(1+sin(v))*cos(u); Y=2*sin(u)*sin(v); Z=sin(2*v); ... plot3d(X,Y,Z,anaglyph=1,n=20,frame=0,scale=1.5,>transparent,grid=20):

This surface is algebraic, its degree being 12. I propose to call this surface, the "Petit russian hat" because of its shape (it is described on Jean-Pierre Petit's web site).
T. Banchoff and his team were studying continuous time dynamical systems when they found the following model, which became rather famous nowadays:
>u=linspace(0,2*pi,50); ... v=linspace(0,2*pi,40)'; ... m=1; a=2; b=1; ... X=(a+b*cos(u)*cos(m*v/2)-b/2*sin(2*u)*sin(m*v/2))*cos(v); ... Y=(a+b*cos(u)*cos(m*v/2)-b/2*sin(2*u)*sin(m*v/2))*sin(v); ... Z=b*cos(u)*sin(m*v/2)+b/2*sin(2*u)*cos(m*v/2); ... plot3d(X,Y,Z,>anaglyph,<frame,scale=1.8,>transparent,grid=20):
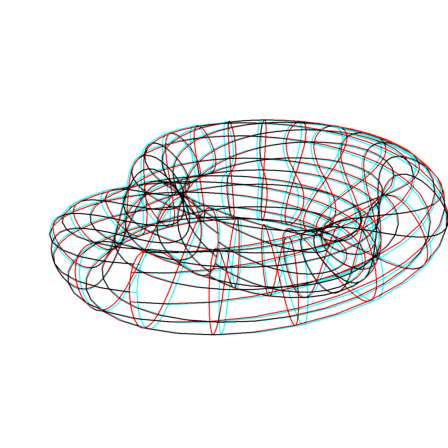
This surface is a sextic. It can be described as a Bernoulli lemniscate turning around an axis and at the same time doing a half-turn around its center. But what if it did THREE half-turns during its revolution?
>u=linspace(0,2*pi,200); ... v=linspace(0,2*pi,200)'; ... m=3; a=2; b=1; ... X=(a+b*cos(u)*cos(m*v/2)-b/2*sin(2*u)*sin(m*v/2))*cos(v); ... Y=(a+b*cos(u)*cos(m*v/2)-b/2*sin(2*u)*sin(m*v/2))*sin(v); ... Z=b*cos(u)*sin(m*v/2)+b/2*sin(2*u)*cos(m*v/2); ... plot3d(X,Y,Z,anaglyph=1,n=20,frame=0,scale=1.8,>hue):

Because of its trefoil-like look surely Escher would have love this one.
Could you find out how the result of sewing a 3-half-turn Möbius band with a 5-half-turn one would like? And maybe find a parametric representation?
And what about the other non-orientable surfaces, for example the one with characteristic -1? (it could look like a sphere with 3 cross-caps, but parameterizing such a surface seems not that easy...)
The Klein-Steiner airways was happy to have you onboard and we are landing now. The external temperature is 30° (the temperature of my brain seems much higher); you can release your seat belts...